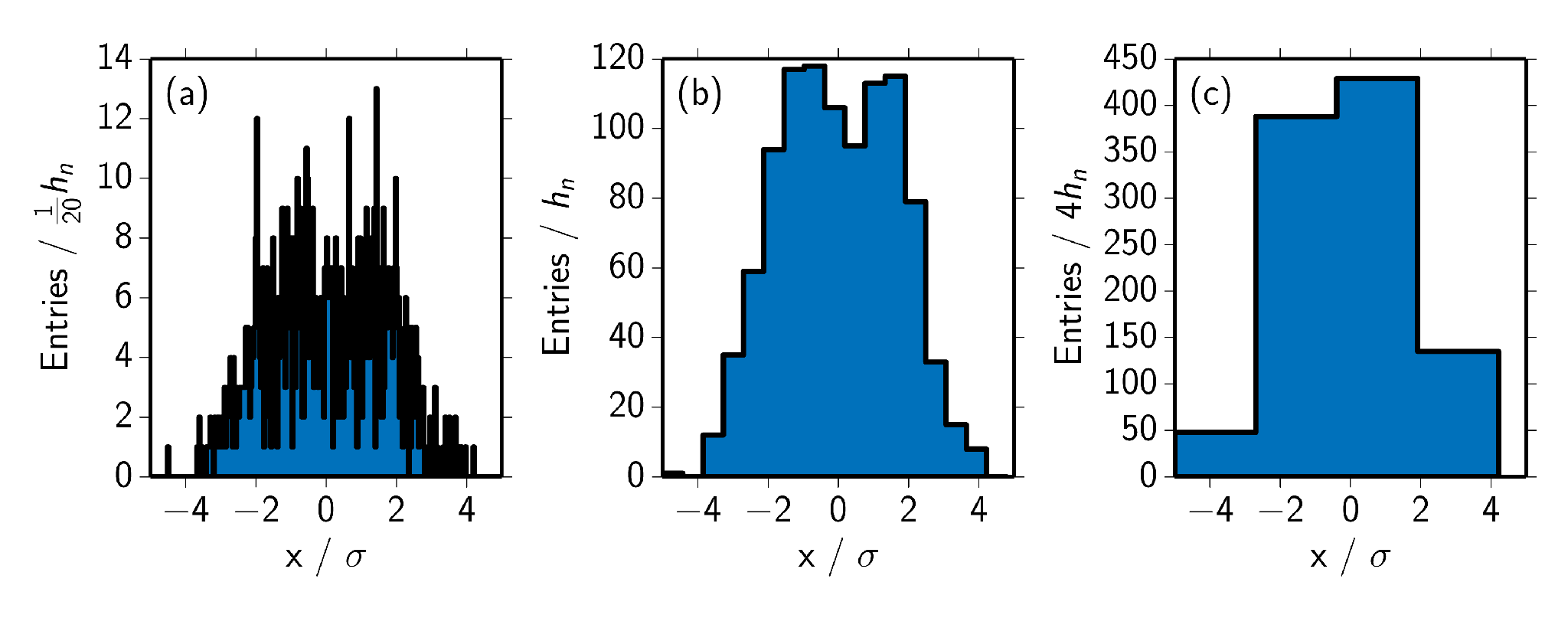
Optimum binning of histograms
Most of the times bin width of histogramms is choosen simply by intuition. However, as the bin-width may heavily influence the interpretaion of the data a more formal coice is needed. While achieving a distribution independent good solution may be a complex task, an often good choice is found by Scott’s rule (D. W. Scott, On optimal and data-based histograms, Biometrika, 1979, 66, 605-610).
Here, the bin-width for data points is given by \[ h_N = 3.49\cdot\sigma\cdot N^{-\frac{1}{3}} \] with the spread of the data . IN the following plot the effect of Scott’s rule is visulazied using random data from 2 normal distributions at . In (a) the bin width is of the optimal bin-sidth, in (b) the bin width is choosen according to Scott’s rule and in (c) the bins are 4 times to large.